| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 통계학개론
- 모수
- 포아송분포
- 모평균
- 기본행연산
- 통계학입문
- 수치형자료
- 표본공간
- 행사다리꼴
- jupyter notebook
- 베르누이분포
- 누적분포함수
- 사조사
- 기댓값과 분산
- 이항분포
- pmf
- 피어슨상관계수
- 이산형
- 확률밀도함수
- 이산확률질량함수
- 조건부확률
- 이변량자료
- 첨가행렬
- Anaconda
- 범주형자료
- 균일분포
- 절삭평균
- 수학적확률
- 표본평균
- 연속확률변수
- Today
- Total
Syeonny의 블로그
분산분석 본문
일원배치 분산분석

앞서 모수의 비교 포스팅에서 두 모평균을 비교하는 방법에 관해 알아보았다.
이번 포스팅에서는 세 개 이상의 모평균을 비교하는 검정방법을 알아보고자 한다.
분산분석 ANOVA
하나의 검정통계량으로 세 개 이상의 모평균을 한 번에 비교하기 위해 분산분석을 이용한다.
분산분석은 ANOVA 아노바, analysis of variance 라고 부르고 있다.
나무위키에서는 '분산분석이란 명목척도로 측정된 독립변수와 등간척도 또는 비율척도로 측정된 종속변수 사이의 관계를 연구하는 통계 기법이다.'라고 정의하고 있다.
이때, 분산분석에서 사용하는 용어 정리는 다음과 같다.
인자: 관측값 혹은 평균에 영향을 주는 특정 조건을 나타내는 변수
인자 수준: 인자가 가지는 값
처리: 각 실험 단위에서 특정한 실험 환경 또는 실험 조건을 가하는 것
처리효과: i번째 처리에서 모평균과 전체 모평균의 차이
오차항: i번째 처리에서 표본과 모평균의 차이
가정
우선, 표본은 독립 이표본과 동일하게 각각의 모집단으로부터 랜덤하게 추출한다.
k개의 모집단이 존재한다면 각각 추출한 표본의 수는 다를 수 있으며, i번째 모집단에서 추출한 표본의 크기는 ni라고 정의한다. 보통 k개의 모평균을 비교하는 경우에 k개의 인자 수준/처리가 존재한다.
이러한 경우에 k개의 모평균 사이에 차이가 존재하는지의 여부를 통계적으로 검정하며, i번째 모집단에서 j번째 확률표본 xij에 관하여 오차항, 모평균, 처리효과를 다음과 같이 정의한다.

만약, k개 모평균의 값이 모두 같다면 전체 모평균도 같은 값을 가지며, 이때의 처리효과는 0이다.
세개 이상의 모평균 비교에 관한 가설은 다음과 같다.
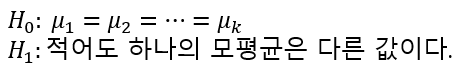
예로 들어 k=3이라면 대립가설의 경우는 다음과 같다.
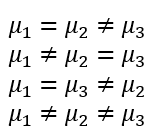
이렇게 가설을 세운 후, 추정된 처리효과의 제곱합을 이용하여 이 값이 크면 귀무가설을 기각하고, 작으면 귀무가설을 기각할 수 없어 채택하는 방식으로 가설검정을 수행한다.
분산분석표
1. 편차의 분해
i번째 표본에서의 편차는 관측값과 i번째 표본의 표본평균의 차이 값이며, 총편차는 관측값과 총평균의 차이 값이다.

2. 변동의 분해
- 총변동 = 총 제곱합 TSS total sum of squares
전체 자료에 대한 산포의 정도를 나타내는 값이다.
총 제곱합은 처리제곱합과 오차제곱합의 합으로 나타낼 수 있다.
TSS = SST + SSE
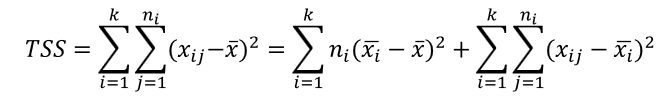
- 처리제곱합 = 처리 간 변동 SST sum of squares of treatment
각 처리의 표본평균과 총평균의 편차의 제곱합이다.
서로 다른 처리를 받은 집단의 중심 위치의 차이를 요약한 값으로 해석할 수 있다.
k개의 처리 평균이 크다면 SST값도 클 것이며, k개의 처리 평균이 작다면 SST값도 작을 것이다.
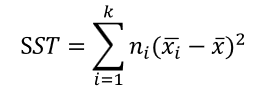
- 오차제곱합 = 처리 내 변동 SSE sum of squares due to error
잔차들의 제곱합으로 정의된 값이며, 각각의 처리 안에서 우연에 인해 나타날 수 있는 변동을 설명하는 값이다.
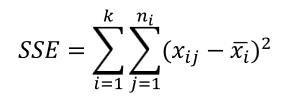
* SST > SSE 이면 처리 효과가 뚜렷하게 존재한다는 뜻으로 귀무가설을 기각할 수 있다. = 대립가설 지지
SST < SSE 이면 처리 효과가 있다는 증거가 미비하다는 뜻으로 귀무가설을 기각할 수 없다.
3. 평균제곱
분산분석은 SST 와 SSE 의 비교를 통해 처리효과, 모평균의 차이를 검정할 수 있다.
이때 f통계량을 사용하는데, SST SSE를 각각의 자유도로 나눈 값의 비율로 나타낼 수 있다.
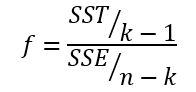
제곱합의 자유도는 제곱합을 구하기 위해 사용한 편차의 개수에서 만족하는 제약조건의 개수를 뺀 것이다.
- 처리평균제곱 MST
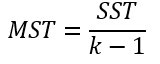
- 오차평균제곱 MSE
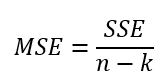
이러한 과정을 통해 분산분석표를 작성할 수 있다.
분산분석표 ANOVA
| 변동요인 | 자유도 | 제곱합 | 평균제곱 | F |
| 처리 | k - 1 | SST | MST | MST/MSE |
| 오차 | n - k | SSE | MSE | |
| 합 | n - 1 | TSS |
가설검정 결론
이렇게 구한 F값으로 맨 처음에 세웠던 가설 검정을 시행할 수 있다.
F값이 크다면 처리의 효과가 있는 것으로 귀무가설을 기각할 수 있다. = 대립가설 지지
F값이 작다면 처리 효과가 없음, 있다는 증거가 없다는 것으로 귀무가설을 기각할 수 없다.
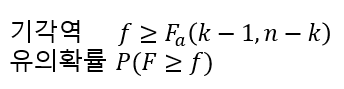
만약, 귀무가설을 기각할 수 있다면 경우에 따라 사후분석 혹은 사후 검정이 필요하다.
/* 틀린 것이 있다면, 댓글을 남겨주세요
출처: 제 4판 통계학입문 [이해와 응용]
*/
'통계학개론' 카테고리의 다른 글
| 회귀분석 (0) | 2023.09.01 |
|---|---|
| 모수의 비교 - 모분산과 모비율 (0) | 2023.08.30 |
| 모수의 비교 - 모평균 (1) | 2023.08.29 |
| 모평균, 모비율, 모분산의 가설검정 (2) | 2023.08.28 |
| 가설검정 (0) | 2023.08.28 |





