| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 연속확률변수
- Anaconda
- jupyter notebook
- 포아송분포
- 이산확률질량함수
- pmf
- 피어슨상관계수
- 수치형자료
- 베르누이분포
- 첨가행렬
- 기댓값과 분산
- 기본행연산
- 통계학개론
- 모수
- 이변량자료
- 통계학입문
- 범주형자료
- 조건부확률
- 사조사
- 행사다리꼴
- 누적분포함수
- 이산형
- 절삭평균
- 수학적확률
- 균일분포
- 이항분포
- 표본공간
- 표본평균
- 확률밀도함수
- 모평균
- Today
- Total
Syeonny의 블로그
공분산과 상관계수 본문
공분산 / 상관계수

이전 게시글에서 두 확률변수의 결합분포에 관해 알아보았다.
이번 게시글에서는 두 확률변수에 관한 공분산과 상관계수를 정의해보려고 한다.
두 확률변수 함수의 기댓값
두 확률변수가 이산형일 때, 결합확률질량함수 p(x, y) 를 가진다.
임의의 함수 g에 관해 기댓값은 다음과 같이 정의할 수 있다.

두 확률변수가 연속형일 때, 결합확률밀도함수 f(x, y) 를 가진다. 기댓값은 다음과 같다.

따라서 임의의 실수 a,b 함수 g,h 에 대해
E(a * g(X, Y) + b * h(X, Y)) = a * E(g(X, Y)) + b * E(h(X, Y)) 임을 정의할 수 있다.
공분산
공분산 (covariance) 은 두 확률변수 X, Y 의 선형관계를 나타내는 양이라고 정의한다.
각각의 확률변수에서 각각의 기댓값을 뺀 값을 통해 구할 수 있다.

만약, X Y가 기댓값보다 큰 값을 갖는다면 위의 식은 양수의 값을 갖는다.
반대로 기댓값보다 작은 값을 갖는ㄴ다면 위의 식은 음수의 값을 갖는다.
이러한 공분산 값을 통해 두 확률변수의 관계와 확률분포의 기댓값을 파악하고, 산점도를 그려 분포의 형태를 이용하여 선형관계를 측정할 수 있다.
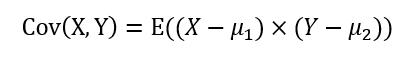
공분산을 구하는 식은 기댓값 성질을 통하여 다음과 같이 나타낼 수 있다.
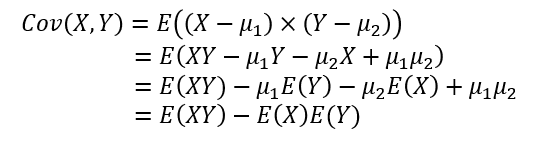
두 확률변수가 서로 독립이면, 공분산의 값은 0이다.
상관계수
상관계수 (correlation coefficient) 는 두 확률변수의 표준편차가 모두 양수의 값을 가질 때, 확률변수를 표준화하여 구한 값으로 두 확률변수의 관계를 파악할 수 있다.
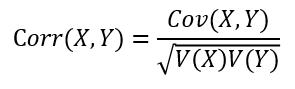
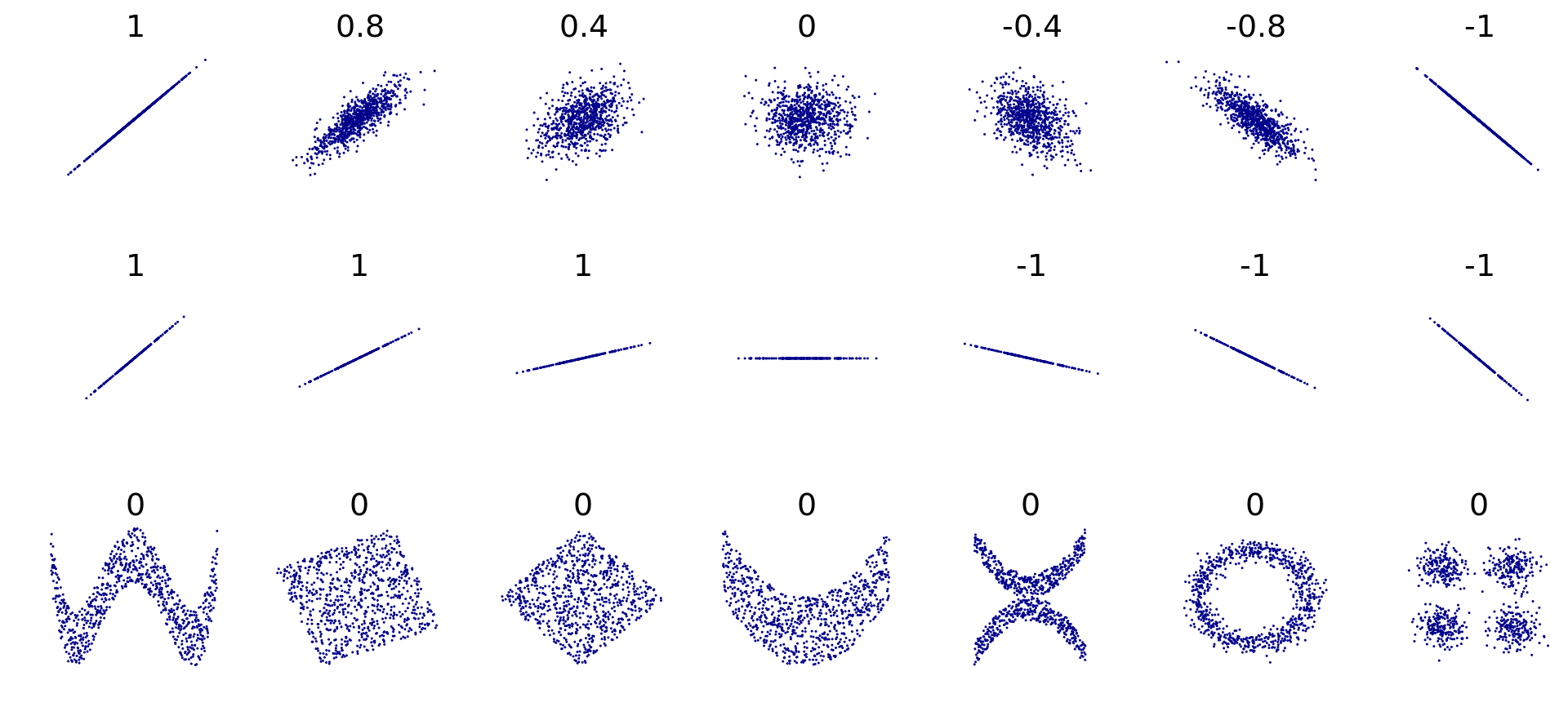
값은 항상 -1 ~ 1을 가지며, 확률분포가 직선의 형태에 가깝게 나타날수록 1에 가깝다.
양수값을 가지면 양의 선형관계, 음수값을 가지면 음의 선형관계, 0이면 선형관계가 없는 것이다.
성질
두 확률변수 X, Y 와 임의의 실수 a, b, c, d에 대해 다음과 같다.
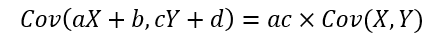
또한, ac의 값이 0이 아니라면
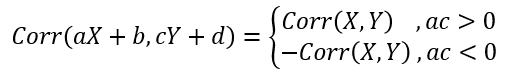
식이 성립한다.
마지막으로, 분산과 공분산의 정의 비교에 따라
Cov(X,X)=V(X) 이기에 다음의 식이 성립한다.
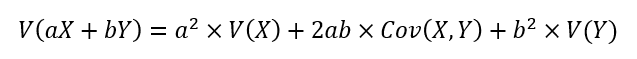
/* 틀린 것이 있다면, 댓글을 남겨주세요
출처: 제 4판 통계학입문 [이해와 응용]
*/
'통계학개론' 카테고리의 다른 글
| 표본 평균과 중심극한정리 (0) | 2023.08.24 |
|---|---|
| 표본추출과 표본통계량 (0) | 2023.08.23 |
| 확률변수의 결합분포 (0) | 2023.08.18 |
| 연속확률분포 - 감마분포 (0) | 2023.08.13 |
| 연속확률분포 - 지수분포 (0) | 2023.08.10 |




