Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- 이산형
- 포아송분포
- 표본공간
- 누적분포함수
- 절삭평균
- 베르누이분포
- 이변량자료
- 이산확률질량함수
- 통계학입문
- 모수
- 행사다리꼴
- 표본평균
- 첨가행렬
- Anaconda
- 모평균
- 확률밀도함수
- 통계학개론
- 범주형자료
- 균일분포
- 사조사
- 피어슨상관계수
- 수치형자료
- pmf
- 기본행연산
- 조건부확률
- 이항분포
- jupyter notebook
- 기댓값과 분산
- 수학적확률
- 연속확률변수
Archives
- Today
- Total
Syeonny의 블로그
최소제곱직선 본문
최소제곱법

점이 존재하고, 내가 고려하는 함수가 존재할 때 함수와 점의 실제 차이를 구하는 방법에 관해 알아보자.
최소제곱직선과 최소제곱법
최소제곱직선은 y값(점)과 함숫값의 차이의 제곱합을 계산해서 후보 함수 중 최소가 되는 최적의 직선을 선택하는 것이다.
최소 제곱 직선은 최소 제곱법을 이용하여 찾을 수 있다.
최소제곱법 ordinary least squares 은?
어떤 계의 해방정식을 근사적으로 구하는 방법으로, 근사적으로 구하려는 해와 실제 해의 오차의 제곱의 합 이 최소가 되는 해를 구하는 방법으로 줄여서 OLS 라고 불린다.

S(a0, a1) 안의 함수가 최소가 되게 해주는 a값들이 argmin이다.
우선 Sxx Syy를 가정하자.

이를 통해 argmin 구하는 과정을 살펴보면 다음과 같다.



결론적으로는
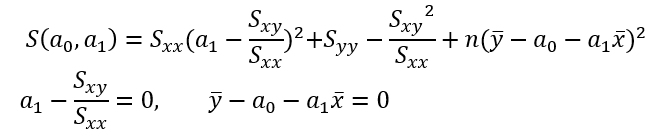
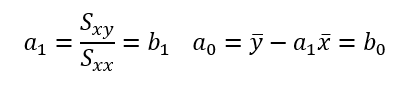
따라서 우리가 최소제곱법을 이용하여 구한 최소제곱직선은 다음과 같다.