| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 포아송분포
- 첨가행렬
- 행사다리꼴
- 이산확률질량함수
- 균일분포
- jupyter notebook
- 범주형자료
- 연속확률변수
- Anaconda
- 사조사
- 표본공간
- 이산형
- 모수
- 피어슨상관계수
- 수학적확률
- 절삭평균
- 통계학개론
- 통계학입문
- 모평균
- 조건부확률
- 확률밀도함수
- 표본평균
- 수치형자료
- 기댓값과 분산
- 누적분포함수
- 기본행연산
- 이항분포
- 이변량자료
- 베르누이분포
- pmf
- Today
- Total
Syeonny의 블로그
머신러닝 기초 (2) 본문
240927
회귀모델 / 분류모델 성능 평가
회귀모델
+ 통계적 지식
회귀분석: 둘 이상의 변수 간 관계를 보여주는 통계적인 방법.
' 관계식을 만들어서 실제 값을 예측 '
단순 선형 회귀 모형 - 표본 회귀 y hat = B0 hat + B1 hat * X
회귀모델에서 우리가 하고자 하는 건: 회귀계수 B0, B1 추정하는 것임
==> 적합값 yi hat = b0+b1*xi
( 표본회귀직선의 추정값 )
- y 실제 값
- y hat 예측값 (보통 우리가 구하고자 하는 모든 예측(추정 값)은 hat이 붙음)
- y bar 평균값
error 가 무조건 존재하는데, 이 error = 오차 를 줄여야 함.
(오차란? 예측 값과 실제 값의 차이 : yhat-y)
예측값이 실제 값과 가까우면 == 당연히 오차는 작은 값은 가짐 ==> 작은 오차를 가지면 당연히 성능이 높아짐
회귀 평가지표
실제 사용하는 평가지표 " 말 그대로 이해 "
- SSE sum squared error
오차제곱합: 오차들의 제곱합 ==> 표본 회귀직선에 가까울 수록 표본 회귀 직선이 주어진 자료 설명을 잘함
yi - yi hat
- SSR sum of squares due to regression
회귀제곱합: 적합값의 편차의 제곱의 합. 추정된 회귀직선으로 설명 가능한 부분
yi hat - y bar
- SST total sum of squared deviations
총 제곱합: SSR + SSE 종속변수의 전체 변동
총 변동/편차 == yi-ybar 제곱 합

- MSE mean squared error
평균오차제곱: 오차 제곱합을 n / n-2 으로 나눈 값
- RMSE
평균제곱근오차: MSE에 root씌운 것
- MAE mean absolute error
평균절대오차: 오차들의 절대값 합의 평균
- MAPE mean absolute percentage error
평균절대비율오차: MAE 비율을 구한 값
- R^2
결정계수: SSR/SST
+)) SSE + SSR = SST
y의 전체 변동 중에서 설명변수 x에 의해 설명되는 부분.
결정계수의 값은 0~1 사이의 값을 가지며, 1에 가까울수록 회귀직선이 data를 잘 설명함.
다중 회귀일수록 결정계수 값은 높아짐
결정계수를 제외하고 나머지 error 가 들어간 회귀 평가 지표는 값이 작아야 한다.
분류 성과지표
정확도를 높이면 됨.
- 혼동행렬
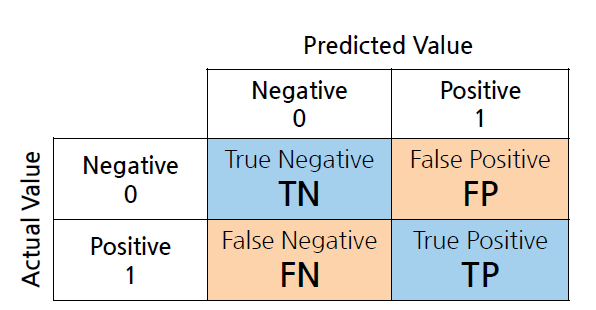
헷갈리지 않는 방법
뒤의 알파벳을 기준으로. P positive N negative 예측
앞의 알파벳은 예측이 긍정 T true 부정 F false
혼동행렬로 평가지표: 비율
- 정확도: 전체 중 예측이 맞은 것
- 정밀도: 긍정(양성)으로 예측한 것 중 긍정인 것
- 재현율, 민감도: 실제로 긍정 중 예측이 긍정인 것
- 특이도: 실제로 부정 중 예측이 부정인 것
F1 score
정밀도와 민감도(재현율)을 하나로 합한 성능평가지표
0~1사이의 범위를 가짐
2 * (정밀도* 민감도 / 정밀도 + 민감도)
++ 추가로 ROC 곡선
x축 혼동행렬의 거짓 긍정률 FP rate
y축 혼동행렬의 참 긍정률 TP rate
그래프가 왼쪽 꼭대기에 가깝게 그려질수록 성능이 우수.
0.7 ~ 0.8 보통
0.8 ~ 0.9 우수
0.9 ~ 1.0 뛰어남
'머신러닝' 카테고리의 다른 글
| 머신러닝 기초 (4) (0) | 2024.10.02 |
|---|---|
| 머신러닝 기초 (3) (1) | 2024.10.02 |
| 머신러닝 기초 (0) | 2024.09.27 |
| [ml] 간단한 정리 (3) (0) | 2024.07.10 |
| [ml] 간단한 정리 (2) (0) | 2024.07.10 |


