통계학개론
모평균, 모비율, 모분산의 가설검정
syeonny
2023. 8. 28. 15:43
모평균 | 모비율 | 모분산

이번 포스팅에서는 모평균, 모비율, 모분산의 가설검정에 대해 알아보고자 한다.
모평균에 대한 가설검정
모평균 μ 에 관한 가설검정 형태는 다음과 같다.

위의 두 가설 형태는 단측검정, 마지막 가설 형태는 양측검정이라 한다.
점추정과 마찬가지로, 모평균의 가설검정에서 모분산을 알고 있을 때와 모를 때 검정방법이 다르다.
모분산을 알 때 모평균의 가설검정의 기각역과 유의확률을 나타내면 다음과 같다.
| 기각역 | 유의확률 | |
 |
||
 |
 |
 |
 |
 |
다음으로 모분산을 모를 때 가설검정은 t분포를 사용한다.
| 기각역 | 유의확률 | |
 |
 |
 |
 |
||
 |
 |

모비율에 대한 가설검정
모평균과 비슷하게 모비율의 가설 검정 형태는 다음과 같다.

모비율은 n이 충분히 클 때 이항분포의 정규근사를 이용한다.


모분산에 대한 가설검정
모분산에 대한 가설검정 형태는 다음과 같다.
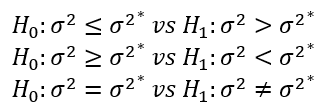
모집단의 분포가 정규분포인 경우에 표본분산은 다음과 같다.

유의확률은 단측검정, 양측검정에 따라 다음과 같이 나타낼 수 있다.

*가설검정은 문제를 많이 풀어보는 게 좋다.
/* 틀린 것이 있다면, 댓글을 남겨주세요
출처: 제 4판 통계학입문 [이해와 응용]
*/






